Note9

Au mur de Planck :

 

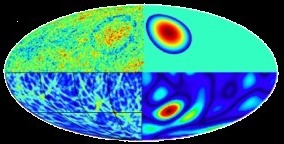
□ L'étude minutieuse du fond diffus de radiations cosmiques (FDC) par l'équipe de chercheurs de la mission Planck a montré que celui-ci n'a rencontré aucun obstacle lors de son expansion, car aucune anisotropie, trace de déformation dûe à une telle interaction, n'a été observée. Ce qui met à mal les théories de Multivers [1]. Une seconde équipe a publié des résultats très robustes, d'une précision de l'ordre de σ(r)=0.009, allant en ce sens [2].

Si l'univers avait interagi avec autre chose lors de son expansion, où s'il était issu d'un autre superunivers, il devrait exister des stigmates résiduels observables dans le fond diffus de radiations cosmiques, or il est d'une accablante homogénéité.

Les données du satellite Planck ont fortement consolidé le modèle Standard.

□L'expansion de l'univers implique qu'il faille une origine à l'espace. La vitesse d'expansion ne pouvant être infinie, il semble  évident que l'univers soit borné. Par abus de langage, on parle parfois d'un espace euclidien concernant l'univers, ou d'un univers hyperbolique ou plat infini, ou encore d'un avant big bang. Un espace ne peut pas être infini, sans bord et continuer de s'étendre, or l'univers est en expansion. Ce qui est visé par là, c'est la topologie globale de l'univers, en tant qu'espace-temps. Car le futur y coexiste avec le passé et le présent : ainsi le paradoxe d'Olbers et le modèle d'univers plat demeurent compatibles. Or, le temps devrait s'arrêter dans 3,7 milliards d'années [3]. 

Lorsqu'il est fait allusion à un univers plat et infini, 

il est question de la topologie de l'espace-temps

projeté dans le futur.

□ Le caractère dynamique de l'espace-temps relativiste implique qu'un espace euclidien physique ne peut pas non plus préexister au big bang, un tel espace ne pouvant pas se déformer [4], car l'orthonormalité est une propriété fondamentale d'un espace euclidien. 

□L'espace émerge et se construit donc par l'effet de quelque chose de plus fondamental. L'univers ne peut par conséquent pas être éternel comme montré par le théorème BVG [5].  

L'espace euclidien que notre cerveau se représente n'est qu'un concept abstrait. Il doit exister une réalité plus profonde. L'espace n'est qu'un matroïde constitué d'informations nues, il est une réalité secondaire.

□ Qu'est-ce que le temps ? Faisons une expérience de pensée. Nommons un univers imaginaire A dans lequel se forme un trou noir aboutissant à notre univers B, un trou noir situé dans notre univers aboutissant de même à un univers C. Un observateur distinct se situe dans chacun de ces univers, nommons-les a, b et c. Selon les mouvements de a, de b et de c, chacun peut consécutivement se situer avant, après ou encore au même instant que les deux autres (cf vidéo infra). Par exemple c se situerait avant a [6], et b se se situerait avant c...

Selon la théorie à inflation éternelle, la vitesse d'expansion agirait en continu de façon différente par région, générant des univers multiples obéissant à des lois variables.

Ainsi, l'univers de c issus de l'univers B précéde celui-ci dans certains cas. Il n'y a donc pas un moment prioritaire absolu situé dans le passé ou le futur : tout est instantané et relatif. À présent, choisissons arbitrairement un instant i0 où les trois extraterrestres observent la naissance de leurs univers respectifs au même instant. Il faudra alors conclure que les trois univers surgissent parallèlement, du mur de Planck, lors du big bang. Ce paradoxe des trois extraterrestres conduit à la conclusion que si il existe un multivers interconnecté, les univers n'obéissent à aucun ordre de priorité à la limite du big bang. 

□Si nous supposons l'existence d'univers multiples qui ne sont pas physiquement interconnectés, il n'y a pas de continuité spatiale ou temporelle les reliant sur une ligne de temps trans-universelle, ils émergent en parallèle, de façon superposée, et il n'y a rien à chercher au delà de leur naissance au mur de Planck. Pas plus qu'il n'y aurait un sens à chercher sur Terre une hypothétique région située plus au Nord du pôle Nord [7]. 

□ Finalement, il ressort que si il existe une multitude de feuilles d'univers, ils surgissent tous du mur de Planck, de manière non locale et superposée. Aucun des univers n'est spatialement extérieur, ou intérieur, ni chronologiquement antérieur ou postérieur à un autre univers, tous sont donc quantiquement superposés et prennent fin au mur de Planck. Car il y a une rupture spatio-temporelle entre les univers distincts hypothétiques. Il n'y a rien à pouvoir chercher de physiquement probable au delà du mur de Planck, car tout l'Univers y prend source, tant spatialement que temporellement.

Approche mathématique 

Structure des infinis 

Proposition 1 — Structure bornée des infinis 

Énoncé

Soit l'ensemble de tous les univers distincts appartenant à une méta-réalité dynamique. On suppose que la création cosmique est un processus continu dans un espace topologique global, et que chaque univers apparaît à un instant appartenant à une chronologie trans-universelle.

Alors, même si |U(t)| diverge, il existe une borne inférieure temporelle telle que :

lim t→t₀⁺ U(t) = ∅ et lim t→+∞ |U(t)| = ∞

Autrement dit, l'existence d'une infinité d'univers n'implique pas une éternité passée : le processus de création peut être infini en cardinalité tout en demeurant fini dans son extension temporelle.

Démonstration

1. Espace de représentation

   Soit une boule fermée de rayon r(t), représentant à l'instant t l'ensemble des univers déjà apparus. On définit une application continue :

   f : T → P(E), f(t) = B(t)

2. Propriétés dynamiques

   On suppose que r(t) est strictement croissante, bornée inférieurement par r₀ > 0 et continue. Chaque univers est représenté par une sphère infinitésimale Sᵢ, l'ensemble étant au plus dénombrable.

3. Limite passée

   Si t → t₀⁺, on a :

   lim t→t₀⁺ B(t) = {O}

   

Ainsi, le système converge vers une limite compacte réduite à un singleton. L'ensemble des univers s'annule continûment à mesure que t → t₀.

4. Infinité sans éternité

   Par le théorème de Cantor, il peut exister une infinité de cardinalités distinctes (ℵₙ) sans qu'aucune ne soit temporellement illimitée. Le processus de création peut donc produire une infinité de mondes dans un intervalle borné de t, tout comme une fonction peut admettre une limite finie malgré une infinité de variations internes.

5. Conclusion

   L'ensemble est infini pour tout t > t₀, mais tend vers le vide lorsque t → t₀⁺. L'infinité des univers est donc convergente dans le passé et divergente dans le futur, sans contradiction avec la finitude de la durée trans-universelle.

Interprétation physique

Élément mathématique Interprétation physique

Ensemble des univers existants à l'instant t Contenu du multivers à l'instant présent

Frontière du présent cosmologique Limite de création (front d'apparition des univers)

Extérieur de B(t) Espaces encore non advenus

Étendue du multivers dans le temps méta-cosmique Amplitude temporelle globale de la création

Origine première, limite inférieure du processus de genèse Instant t₀ — point zéro des émergences

Ainsi, l'infini cosmique est quantitatif, non chronologique : il exprime la richesse du possible, non l'éternité du passé.

---

Proposition 2 — Structure atemporelle des ensembles infinis d'univers

Énoncé

Soit l'ensemble de tous les univers possibles, distincts mais non reliés par une chronologie commune. On suppose qu'il n'existe aucune métrique temporelle globale sur U, c'est-à-dire :

∄ t: U→ℝ

Alors :

1. U peut être modélisé par un espace compact non métrisable ou une variété fractale de dimension fractionnaire ;

2. sa densité peut croître localement sans expansion temporelle ;

3. et toute création observée dans un univers particulier résulte d'un déploiement interne de potentialités, non d'une succession causale inter-universelle.

Démonstration (esquisse)

1. Structure topologique

   Sans ordre global, U n'est pas un espace métrique au sens habituel, mais peut être muni d'une topologie de recouvrement local : pour chaque univers uᵢ, il existe un voisinage Vᵢ contenant des univers partageant une structure physique ou ontologique commune.

2. Densification

   On définit une fonction de densité locale :

   ρ(uᵢ) = lim ε→0 |Vᵢ(ε)|/μ(Vᵢ(ε))

   Cette densité peut varier sans que cela traduise une évolution temporelle — elle exprime simplement la répartition structurelle du possible.

3. Absence d'éternité et d'origine

   Dans cette configuration, aucune limite inférieure ne peut être définie ; il n'existe donc ni commencement ni fin global. L'espace est auto-contenu : chaque univers possède sa propre métrique interne du temps, mais aucune métrique commune ne lie ces temps entre eux.

   ∀ uᵢ, uⱼ ∈ U, tᵢ ≢ tⱼ

4. Compactification conceptuelle

   Par analogie, U peut être considéré comme une variété compacte de dimension fractionnaire : la structure globale est finie (compacte), mais son contenu est indénombrable, dense et localement infini. La création devient un phénomène d'actualisation locale de potentialités distribuées, et non d'ajout successif d'éléments.

Interprétation physique et philosophique

Élément mathématique Interprétation physique

Ensemble des univers possibles, sans lien causal global Multivers sans chronologie commune

Densité ρ(uᵢ) Niveau de proximité ontologique entre univers similaires

Compactification Finitude structurelle du possible, sans temps commun

Absence de global t Atemporalité du multivers, simultanéité potentielle de toutes les formes d'être

Fractalité Hiérarchie interne de possibilités, auto-réplicante et non séquentielle

Dans ce modèle, l'infini n'est plus directionnel, mais distribué : chaque univers contient, sous une forme potentielle, la totalité des autres, selon une structure d'imbrication auto-similaire. Il n'y a ni « avant » ni « après », seulement des zones d'actualisation au sein d'un espace de possibles atemporel.

---

Idée centrale (informelle)

Dans un multivers sans chronologie trans-universelle, chaque petit voisinage ontologique (ou « site » local) possède sa propre séquence d'actualisations (les univers « surgissent un à un » localement dans U). Ces séquences sont locales et totales à l'intérieur de chaque voisinage, mais il n'existe pas d'ordre commun global. Ainsi, les actualisations sont parallèles globalement mais séquentielles localement.

---

Trois modèles rigoureux équivalents

Modèle A — Famille indexée de lignes temporelles

· Soit un ensemble d'indices représentant les sites locaux

· Pour chaque x, on associe une ligne temporelle totale Eₓ = {eₓ,ₙ} et une suite d'événements représentant les actualisations successives d'univers en x

· Il n'existe pas de relation d'ordre total entre Eₓ et Eᵧ si x ≠ y. On obtient donc une famille de temps locaux

· Chaque univers appartient à un unique événement (ou à un petit sous-ensemble)

Globalement : les événements forment un ensemble partiellement ordonné avec seulement des ordres locaux.

Avantage : clair et simple à manier.

Inconvénient :ne rend pas naturellement la proximité topologique.

Modèle B — Ordre partiel et foliations

· L'espace des univers est muni d'une topologie locale

· On définit une relation d'antériorité partielle sur les événements telle que, pour tout voisinage Vₓ, la restriction de cette relation soit un ordre total

· Pour deux événements situés dans des voisinages disjoints, la relation n'est pas définie (éléments incomparables)

· Mathématiquement, (E, ⪯) est un poset qui se feuillette en feuilles totalement ordonnées locales

Avantage : exprime la continuité locale et la non-comparabilité globale.

Outils :théorie des feuilletages, topos, catégories fibrées.

Modèle C — Processus stochastique local

· Pour chaque site x, on considère un processus ponctuel (par ex. de Poisson) sur une échelle locale τₓ. Les sauts de ce processus correspondent aux surgissements d'univers

· Les processus {Pₓ} sont indépendants (ou faiblement corrélés localement) et sans axe temporel commun

· Cela formalise l'idée de « un à un localement » et « en parallèle globalement »

Avantage : utile pour modéliser un phénomène d'émergence stochastique.

Inconvénient :introduit un caractère probabiliste non toujours souhaité.

---

Propriété formelle utile (Proposition synthétique)

Proposition (émergence locale séquentielle, parallélisme global).

Soit un espace topologique de sites locaux X.Pour chaque x ∈ X, soit Eₓ = { eₓ,ₙ } un ordre total (ligne temporelle locale) et la suite d'événements d'actualisation en x. Alors l'union

E = ⨆ₓ∈ₓ Eₓ, eₓ,ₙ ⪯ eₓ,ₘ si n ≤ m (même x)

forme un ensemble partiellement ordonné localement total.

Preuve : immédiate par construction (réflexivité, antisymétrie, transitivité sur chaque feuille).

---

Conséquences et clarifications conceptuelles

1. Pas de contradiction logique

   « Un à un localement en parallèle » n'est pas paradoxal : les ordres locaux sont simplement non comparables.

2. Causalité interne préservée

   Chaque univers garde sa propre métrique temporelle. Aucune cause trans-universelle n'est créée.

3. Comparaisons locales possibles

   Si deux sites sont topologiquement proches, on peut introduire des morphismes ou correlations pour exprimer des couplages faibles — restituant un quasi-ordonnancement local.

4. Outils mathématiques pertinents : posets, feuilletages, fibrations, topos, processus ponctuels, réseaux de Petri.

 _________________

[1] M. Tristram, A. J. Banday, K. M. Górski, R. Keskitalo, C. R. Lawrence, K. J. Andersen, R. B. Barreiro, J. Borrill, L. P. L. Colo

mbo, H. K. Eriksen, R. Fernandez-Cobos, T. S. Kisner, E. Martínez-González, B. Partridge, D. Scott, T. L. Svalheim, I. K. Wehus. Improved limits on the tensor-to-scalar ratio using BICEP and Planck. arXiv:2112.07961 [astro-ph.CO] (or arXiv:2112.07961v1 [astro-ph.CO] 

[2] BICEP/Keck Collaboration: P.A.R. Ade (1), Z. Ahmed (2), M. Amiri (3), D. Barkats (4), R. Basu Thakur (5), D. Beck (2,7), C. Bischoff (6), J.J. Bock (5,8), H. Boenish (4), E. Bullock (9), V. Buza (10), J.R. Cheshire IV (9), J. Connors (4), J. Cornelison (4), M. Crumrine (11), A. Cukierman (7,2), E.V. Denison (12), M. Dierickx (4), L. Duband (13), M. Eiben (4), S. Fatigoni (3), J.P. Filippini (14,15), S. Fliescher (11), N. Goeckner-Wald (7), D.C. Goldfinger (4), J. Grayson (7), P. Grimes (4), G. Halal (7), G. Hall (11), M. Halpern (3), E. Hand (6), S. Harrison (4), S. Henderson (2), S.R. Hildebrandt (5,8), G.C. Hilton (12), J. Hubmayr (12), H. Hui (5), K.D. Irwin (7,2,12), J. Kang (7,5), K.S. Karkare (4,10), E. Karpel (7), S. Kefeli (5), S.A. Kernasovskiy (7), J.M. Kovac (4,16), C.L. Kuo (7,2), K. Lau (11), E.M. Leitch (10), A. Lennox (14), K.G. Megerian (8), L. Minutolo (5), L. Moncelsi (5), Y. Nakato (7), T. Namikawa (17), H.T. Nguyen (8), R. O'Brient (5,8), R.W. Ogburn IV (7,2), S. Palladino (6), T. Prouve (13), C. Pryke (11,9), B. Racine (4,18), C.D. Reintsema (12), S. Richter (4), A. Schillaci (5), B.L. Schmitt (4), R. Schwarz (11), C.D. Sheehy (19), A. Soliman (5), T. St Germaine (4,16), B. Steinbach (5), R.V. Sudiwala (1), G.P. Teply (5), K.L. Thompson (7,2), J.E. Tolan (7), C. Tucker (1), A. Turner (8), C. Umilta (6,14), C. Verges (4), A.G. Vieregg (20,10), A. Wandui (5), A.C. Weber (8), D.V. Wiebe (3), J. Willmert (11), C.L. Wong (4,16), W.L.K. Wu (2), H. Yang (7), K.W. Yoon (7,2), E. Young (7,2), C. Yu (7), L. Zeng (4), C. Zhang (5), S. Zhang (5) ((1) Cardiff University, (2) KIPAC/SLAC, (3) University of British Columbia, (4) Harvard/CfA, (5) Caltech, (6) University of Cincinnati, (7) Stanford University, (8) NASA JPL, (9) Minnesota Institute for Astrophysics, (10) University of Chicago, (11) University of Minnesota, (12) NIST, (13) SBT Grenoble, (14) University of Illinois at Urbana-Champaign, (15) University of Illinois at Urbana-Champaign, (16) Harvard University, (17) The University of Tokyo, (18) Aix-Marseille Universite, (19) Brookhaven National Laboratory, (20) University of Chicago), BICEP / Keck XIII: Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season. DOI :10.1103/PhysRevLett.127.151301Cite as:arXiv:2110.00483 [astro-ph.CO] (2021)

[3] Raphael Bousso, Ben Freivogel, Stefan Leichenauer, Vladimir Rosenhaus. Eternal inflation predicts that time will end. Phys.Rev. D83:023525 (2011). DOI: 10.1103/PhysRevD.83.023525 Cite as: arXiv:1009.4698 [hep-th], (or arXiv:1009.4698v1 [hep-th] for this version)

[4] Si l'espace était euclidien, il faudrait qu'absolument tout objet occupant l'univers exerce envers strictement chacun des autres objets peuplant l'univers pris un à un, une force d'attraction magique directement proportionnelle au produit de leurs masses respectives, et inversement proportionnelle au carré de la distance qui les sépare deux à deux. Ainsi rien que pour les seules étoiles de la partie observable de l'univers, une telle probabilité serait de l'ordre de 1/(10¹¹)¹⁰¹¹. Comment expliquer un tel effet, sans oublier que cela dure dans le temps ? Un tel nombre à 3 étages de puissances défie l'entendement, le principe de parcimonie implique donc d'exclure l'hypothèse d'un espace euclidien intemporel existant physiquement.

[5] Borde, A. H. Guth, A. Vilenkin, (15 April 2003). "Inflationary space-times are incomplete in past directions". Physical Review Letters. 90 (15): 151301. Bibcode : 2003PhRv arXiv:grqc/0110012 90o1301B. doi:10.1103/PhysRevLett.90.151301. PMID 12732026.

[6]  Juan Maldacena & Leonard Susskind, Cool horizons for entangled black holes. (2013) 48 pages, 23 figures. v2: references Subjects : High Energy Physics - Theory (hep-th) DOI:10.1002/prop.201300020 Cite as:arXiv:1306.0533 [hep-th] (or arXiv:1306.0533v2 [hep-th] for this version)

[7] En choisissant que a, b et c sont à une distance identique et suffisamment proches des trou noirs respectifs pour ce qui est de a et de b, strictement toutes les configurations sont possibles suivant que nos extraterrestres se placent avant ou après les trou noirs marquant la naissance des autres univers. À savoir ; {a,b,c}, {a,c,b}, {b,a,c}, {b,c,a}, {c,a,b}, {c,b,a}.